Locality is the state of affairs confined to us (at least macroscopically); blame special relativity and the finite speed of light. Oh sorry, you might not have heard of what locality is yet have you? It means anything I do; I can only influence my future up to the fastest influences that we can ever achieve: light speed. Locality is the limit for events in one point of space-time to influence another in a causation relationship.
Whatever that I do now cannot possibly cause the volcanoes of planets light years away to explode immediately (ignoring the possibility to warp space-time using general relativity which is out of the scope of this discussion). So sorry to disappoint you, but all those telepathy stuffs you see in science fiction, they are just that: fantasies.
“Wait a minute,” you said, “hasn’t quantum physics lead us to the discovery of quantum entanglement (which is non-local), so it means that there is a remote possibility that telepathy can happen right?” Well, the answer to that is still, even through you can have non-locality, you still cannot communicate faster than the speed of light. There are various proofs for the impossibility for using quantum non-locality to communicate faster than the speed of light, but it is not in the scope of the discussion here too. The scope of this discussion how the notion of non-locality affects the way we review and research about the foundations of quantum physics.
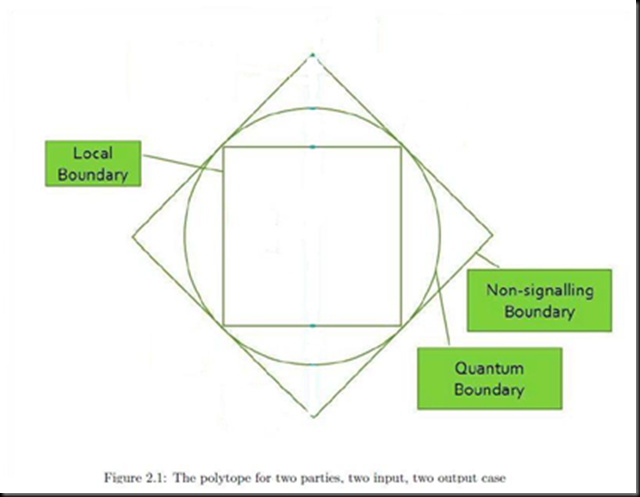
Now that you know what is locality, non-locality simply means that events influence each other, even when they are so far apart that light cannot reach from one event to another in time! However, there is also the constraint of not able to communicate using non-locality. This means that there is an interesting space in the relationships between any two parties, a space between the usual local region that we are used to and faster than light communication region (signalling region). A space we call the non-local region. Refering to the figure below, one can construct a polytope (essentially a geometrical object representing probabilities) that maps the local region inside the nonsignalling region. The quantum boundary (representing the limits of quantum entanglement) exists and extends beyond the local region but falls short of the non-signalling boundary.
Let me explain more of the figure above, the two parties each can choose one of two inputs into a machine that they share, and the machine (defined by whatever properties that the analysis below requires it to have) gives out one of two outputs at each side. One iron rule is that they cannot communicate. The correlations of the output depending on the input can be quantified and represented in the polytope above. The local region of the polytope consists of the correlations that two parties can have with only preestablished agreement (for the machine). For the quantum region, the two parties share quantum entangled particles in addition to preestablished agreements. However, theorectically speaking, one can still have stronger correlations between the two without the ability to start communication between the two parties. Hence, the Non-signalling boundary is bigger than the quantum boundary. Therefore, although quantum physics is non-local, it is not the most non-local theory allowed by special relativity. Here a clue of how nature works is found and the clue is to ask why?
Before continuing, we shall have a small detour to the current state of quantum physics. You see, the postulates of quantum mechanics as it stands now are just a sequence of abstract mathematical rules to calculate and predict the probabilities of the results of measurements. Confused? Worry not, even the great Feynman said no one truly understands quantum mechanics. Sure, we can calculate and predict and give a very good and consistent picture of the world, but we do not know the underlying “why” of quantum physics. The underlying physical picture that is intuitive in all other areas of physics is not clear at all in quantum physics.
So encountering this clue, researches proposed various theories to be the information-theoretic axiom for quantum mechanics. These theories seek to limit the bound of non-locality any general theory must have and tries to reproduce the bounds of quantum physics using as little axioms as possible.
One of the axioms that do this is the information complexity triviality axiom. It states that to share information from one party to another, one (normally, under locality assumption) has to share all the bits of the information. One example is that one has to download a full movie to enjoy it. With quantum non-locality, the amount of bits sent is reduced; however, it is still a significant amount that needed to be sent. With even stronger correlations above a certain bound (called communication complexity bound) [1], the amount of information sent reduces just to one bit! Imagine watching a movie or for that matter, downloading the whole of internet in just one bit! Computer scientists would say that this is as forbiddened as non-conservation of energy [4]!
Therefore, non-local physical theories cannot be above the communication complexity bound. However, communication complexity bound is not the same as the quantum theory bound. If we can somehow pull down the communication complexity bound down to the quantum theory bound, we have found a physical axiom for quantum physics! And the way to do this is via non-locality distillation [2].
As implied by its name, non-locality distillation makes an existing non-local correlation to become more even more non-local. That is it pushes the point of correlation away from the centre of the polytope. Imagine that the line (collections of points) just above the quantum bound is being distilled. If they can go up to and beyond the triviality bound, the triviality bound is effectively “lowered” down to the quantum boundary.
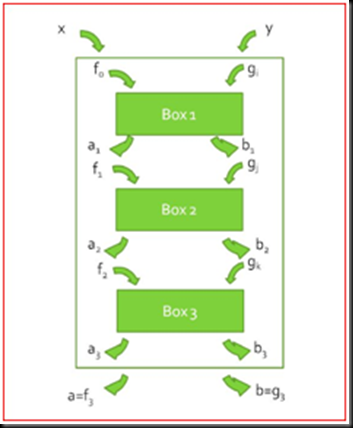
How the distillation is done is that two (or more) non-local correlation “machines” are brought together and the output of one is wired up or linked up in a certain way to the input of the other to produce one big “machine” with more overall non-locality. We denote each wiring as one protocol. It was shown that two boxes could not be used to achieve this feat [3]. That was where the author's humble attempt comes in. Using three boxes, the author has attempted to achieve this feat. The attempt is aided by aiming to find a protocol to achieve a victory condition that was defined. The result was that two resonable and symmetric victory conditions were ruled out as no protocols are able to statisfy them. A general mechanism is found to allow for the determination of which protocol (amongst all 4.61x1016 possible protocols) is able to achieve any victory conditions.
In addition, it would seem that it is not worth the effort of pursuing more boxes distillation research as the amount of protocols, terms and conditions will increase exponentially with the number of boxes.
Regardless of this line of research, the story goes on with Stephanie Wehner of Centre for Quantum Technologies who had just recently managed to link the quantum boundary with Heisenberg uncertainty principle. This means that quantum theory is as non-local as it is because of the Heisenberg uncertainty principle, which is also an empirical fact. So in essence, the mystery of the quantum is still there. Is there any fundamental axiom that fixes quantum physics? Will we ever get an intuitive understanding of it? It is up to you to find out.
Ng Xin Zhao (27th Jan 2011, year 3 undergraduate student in Physics, NUS)
Bibliography
[1] Gilles Brassard, Harry Buhrman, Noah Linden, Andre Allan Methot, Alain Tapp, and Falk Unger Limit on nonlocality in any world in which communication complexity is not trivial. Phys. Rev. Lett., 96(25):250401, Jun 2006.
[2] Nicolas Brunner and Paul Skrzypczyk. Nonlocality distillation and postquantum the-ories with trivial communication complexity. Phys. Rev. Lett., 102(16):160403, Apr 2009.
[3] Anthony J. Short. No deterministic purification for two copies of a noisy entangled state. Phys. Rev. Lett., 102(18):180502, May 2009.
[4] W. van Dam. Implausible consequences of superstrong nonlocality.
http://arxiv.org/quant-ph/0501159, 2000.